《线性声学基本现象》Chapter 9-第九章：共鸣 第三部分

CAE大拿

  《线性声学基本现象》

       MSC软件官方微信独家连载的一系列声学理论知识中，帮助国内关注声学应用的工程师，科研人员，高校老师，企业管理者等学习了解声学。各位读者看到的如下系列声学知识连载，是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique  linéaire》（《线性声学基本现象》）的中文翻译。

《线性声学基本现象》-总第21期

Chapter 9-第九章：共鸣  第三部分

（请关注MSC官方微信查看往期内容，微信号：MSCSoftware。）

---

      本章会讲到在所有的封闭声场中都将产生声学的共鸣现象 (acoustic resonance)。我们首先使用简单的声学管道引入特征频率和特征模态的概念。随后，我们还将介绍声学模态叠加，即管道中的声场可以表示为特征模态的线性叠加。使用同样的模态叠加概念，我们也可以用解析的方法得到长方体声学空腔中的声场分布。对于任意形状的声学空腔，我们可以使用数值模态的方法表示其声场分布。
      在接下来的第十章，我们还会进一步介绍亥姆霍兹共鸣器与四分之一波长共鸣器。

9.1 封闭管道中的共鸣

9.1.1  速度源激励

        图9.1表示一个长度为l的水平管道。以此图的上半部分为例，我们看到管道左端一活塞物体以速度v(ω)做水平振荡。管道右端为固壁边界条件，即法向速度等于零。

图9. 1：右端封闭的管道其左端受到不同类型的激励，上图为速度源激励，下图为压力源激励

       我们假设管道内的声场分布仅在水平方向产生变化（一维声场假设），那么声压可以写成如下形式：

声学速度的表达式则为：

根据对于管道两端边界速度条件的描述，我们已知：

此时再套用公式9.2至边界条件中，可以得到由声压幅值表示的边界条件：

我们对上式进行求解，可以得到声压的解，进而再通过9.2式得到速度的解：

当kl的取值为零或为π的倍数时，管道内的声压趋向于无穷大，此时存在如下关系：

当管道的长度等于二分之一波长的整数倍时，管道中会发生共鸣。

9.1.2  声压源激励

        考虑同样的管道，并在左端用压力源替代速度源。假设我们使用某种设备可以在左端提供一个振荡声压的固定幅值p(ω)。管道内的声压与速度表达式依然可以写为之前的形式：

由于声源的变化，边界条件变化为：

将9.8式和9.9式带入边界条件表达式中，得到以声压幅值表示的边界条件：

通过以上方程组，求解得到的声压与速度在管道中的解为：

当cos(kl)取值为零时，声压趋向无穷大。此时存在如下关系：

当管道的长度等于四分之一波长的奇数倍时，管道中会发生共鸣。

9.1.3 速度源与压力源的比较

        无论对于速度源或是压力源，声学阻抗Z均是管道的内在特性：

共鸣现场产生的频率取决于管道的特性以及声源的特性。我们比较由速度源激励产生的共鸣频率（公式9.7）和由声压源激励产生的共鸣频率（公式9.14），可以发现两者之间相差的频率间隔为c/4l。图9.2显示了管道中声场的频率特性，在粗线（速度源激励）与细线（压力源激励）的频谱之间相差了如上的频率间隔。

图9. 2：右端封闭管道中声压的频率响应 （管道长度 l=1m, 声速c=340m/s， 声压在x= 0.707m处计算）。粗线为速度源激励，细线为声压源激励。

         为了理解两种声源情况的区别，我们首先要弄清共鸣状态下声场趋于无限大的原因。

         首先考虑速度源激励。在管道中同时存在由速度源产生的直接声场（pie-ikx）以及被另一侧封闭端反射回的声场（pie+ikx）。除此之外管道中还会存在反射声场再次接触到管道两端的再次反射，以及更多次的循环反射。在共鸣频率以外，所有的声波相互叠加时存在彼此削弱的现象，因此声压的数值是有限的。而在共鸣频率处，声波叠加时会彼此加强，导致声压数值趋向无穷。当声波经历的路程（由一处传到另一端并被反射回原处）是波长的整数倍时，声波的叠加会彼此加强。因此当管道的长度为半波长的整数倍时便会产生共鸣。

        下面考虑声压源激励的情况。如同上一种情况，在管道中同时存在由速度源产生的直接声场（pie-ikx）以及被另一侧封闭端反射回的声场（pie+ikx）。然而，反射声场在激励端被再一次反射时将产生180度的相位变化（-pie-ikx）。只有在声波两次反射经历的路程为半波长的奇数倍时，最初的直接声场才会与两次反射后的声场产生叠加加强的效应。由此可知，当管道的长度为四分之一波长的奇数倍时会发生共鸣。我们可以从另一个角度看待声压源激励，把它对声波的反射看成在传播路径上加入了半个波长的距离。

        我们也可以用一种几何的方式解释上述问题。如果我们使用一声压幅值固定的声压源在管道左侧进行激励，我们知道此固定声压幅值一定是有限的。在共鸣发生时，声压最大值（共鸣点）的位置一定是左端向管道内部进入一段距离的位置，我们将此处的坐标设为xmax，即此点到左端的距离。不论左端施加激励的声压值为多大，这个固定的幅值相对于共鸣位置的声压幅值均是无限小的，因此这两点之间的距离即xmax一定趋近于四分之一波长。接下来再看管道的另一端，由于固壁边界的存在右端的声学速度为零，即声压对位置坐标的导数为零，也就是说这一端声压幅值一定也位于波峰或波谷的顶端。因此结合前面的分析，管道的长度一定为左侧第一个共鸣位置到右端的距离（半波长的整数倍）再加上左侧共鸣位置到最左端的四分之一波长，也就是说管道总长度等于四分之一波长的奇数倍。

        我们也可以使用同样的方法考虑速度激励的情况：最左端速度激励相当于将此处声压对位置坐标的导数固定。然而随着多次反射的声压产生正向叠加，最大声压发生的位置趋向于管道最左端。于是在管道最左端距离激励点无限近的距离产生最大声压（导数为零）。在管道的最右端，固壁条件及声压对位置导数为零的条件同样存在。因此共鸣发生时，管道的长度一定是半波长的整数倍。

        关于声压源与速度源的概念以及对比还会在下一章中进行讨论，届时我们会引入声源阻抗的概念。

9.2 特征模态与特征频率

两端闭口管道

      考虑一长度为l且两端均封闭的管道，在没有任何激励的条件下，两侧的固壁边界条件可以表示为：

满足上述方程的解为p+=p-且e-ikl=e+ikl。对于第二个等式关系，其成立条件为：

可见，即使不存在任何激励源，共鸣频率仍然存在。从理论上讲，在共鸣频率即使声源关闭，声音仍然可以无限制延续。

管道中第n阶共鸣频率下的声场分布为：

这里的共鸣频率值为f=nc/2l。

一端开口，另一端封闭的管道

        在较低的频率区间，管道的开口端条件可以近似使用声压为零替代。左端开口，右端封闭管道的边界条件为：

同样可以表示为

满足上述方程的解为p+=-p-且e-ikl=-e+ikl。对于第二个等式关系，其成立条件为：

管道中第n阶共鸣频率下的声场分布为：

两端开口管道

       对于两端开口的管道，边界条件为：

同样可以表示为

满足上述方程的解为p+=-p-且e-ikl=e+ikl。对于第二个等式关系，其成立条件为：

管道中第n阶共鸣频率下的声场分布为：

下面的图9.3显示了三种不同边界条件管道内的声压模态：

图9. 3：不同管道内前四阶模态的声压分布。上图：两端封闭；中图：两端开口；下图：左端开口、右端封闭

9.3 模态的叠加

         在左端受速度源激励、右端封闭的管道中，声压分布的表达式为：

如上的声压分布可以近似表示为两端封闭管道中声压模态的线性叠加：

下面需要求解各阶模态的参与因子An。将上式两侧均乘以cos(mπx/l)，并在[0,l]这个区间内进行积分。对于如下积分：

当m与n不相等时，其积分值为零；当m与n相等且不等于零时，其积分值为l/2；当m与n都等于零时，其积分值为l。于是再结合9.27式，可以计算得到各阶参与因子：

        下面的图9.4显示了声压精确值与模态叠加近似值的对比。随着模态阶数的增加，模态叠加的声压迅速趋向于精确值。当然在x=0的位置两者之间始终存在差距。这是由于模态声压的计算假设了x=0位置的速度为零，这与真实的速度源激励显然不同。图9.5显示了速度解的对比，在x=0处精确解与模态叠加的结果差距更明显一些。

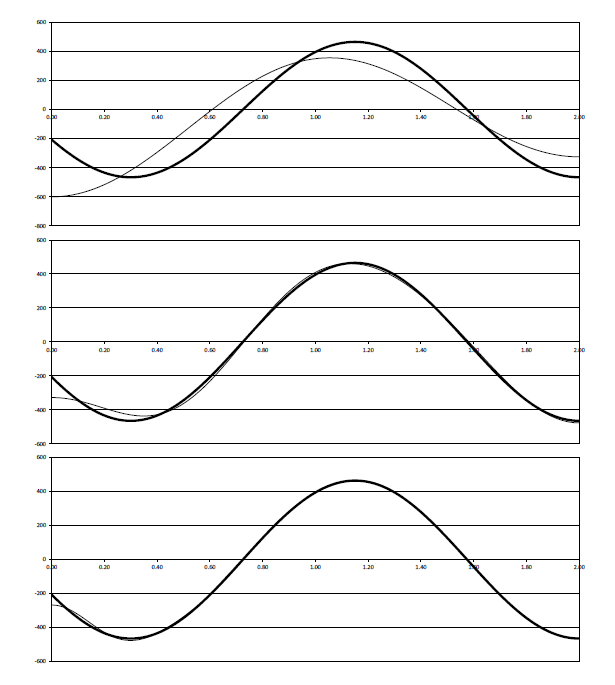
图9. 4：管道中的声压分布（l=2m, f=200Hz, 速度激励源幅值 v=1m/s ）：对比声压的精确值（粗线）与模态叠加的近似值（细线）。上图：选取前2阶模态；中图：选取前5阶模态；下图：选取前10阶模态

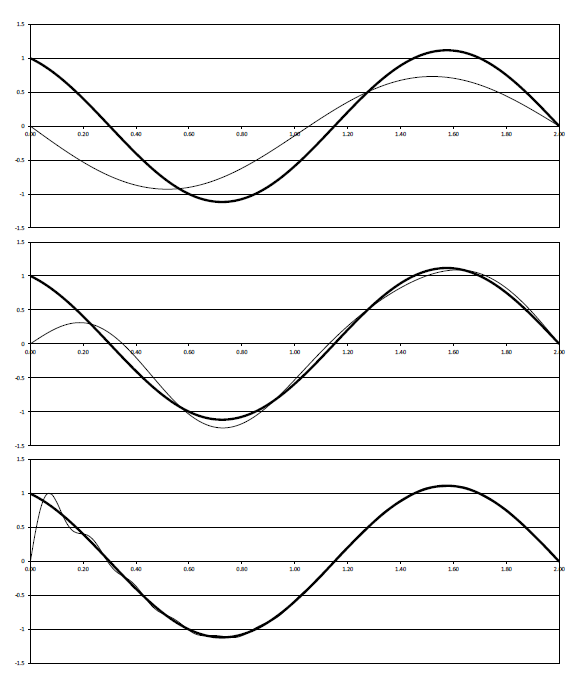
图9. 5：管道中的速度解分布（l=2m, f=200Hz, 速度激励源幅值 v=1m/s ）：对比速度解的精确值（粗线）与模态叠加的近似值（细线）。上图：选取前2阶模态；中图：选取前5阶模态；下图：选取前10阶模态

9.4 长方体声腔的模态

       假设一长方体声腔的三边为a * b * d, 其所有边界均为固壁条件。为了计算其共鸣模态，我们需要使用三维的亥姆霍兹方程：

其在三个维度的固壁边界条件为：

空间中声压的解可以写成如下形式：

且如下关系成立：

当

三个方

向的波数可以表示成下式时，可以满足固壁边界条件：

每组角标的组合(i,j,m)对应一阶特定模态的空间分布：

模态的频率表达式为：

图9.6显示了长方体声腔中的三个不同模态。

9. 6：一长方体声腔中的三个不同模态

在0Hz的模态
在0Hz的模态阶数为i=j=m=0，其对应腔体空间内各点等值的声压分布。这个声学模态类似于结构动力学中的刚体模态。回顾前面的图9.2，在低频出现的较高声压响应就是由此模态产生的。

9.5 任意形状声腔的模态

       对于任意形状声腔的模态，可以使用有限元（finite element method）的方法计算求得。考虑一个具有固壁边界的腔体Ω，有限元方法得到的系统方程为：

        其中K，C，M分别表示系统的刚度、阻尼与质量矩阵，向量p代表各有限元节点的声压，向量F代表激励源。若不考虑阻尼与激励，系统方程则简化为：

        如上齐次方程具有一组非零解，并对应一组特征值 ω=ωi。每个特征值对应一种特定的声压分布φi，称为特征模态。特征值对应的特征频率为fi=ωi/2π。下图9.7以一汽车空调腔体单元为例，显示了用有限元方法计算的腔体模态。

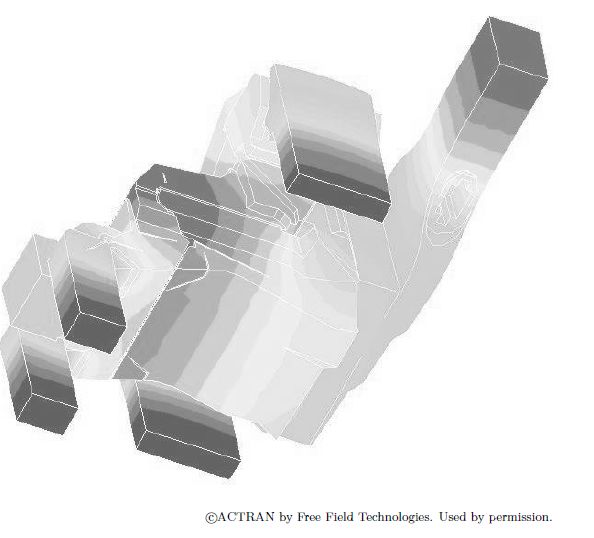
9. 7：一空调腔体单元的声学模态，模态频率 f =444Hz